To many, modern mathematics and Africa are not synonymous. Open any school mathematics book and the role of African scholars has been relegated to the category of ‘ethnomathematics’, as if mathematics here was in some way linked to tribalism. The contribution of African women to the development of mathematics has also been relegated to the sidelines. However, the Sub-Saharan sona patterns, or sand graphs, which forms part of modern knot theory, is used in very important branches of pure and applied mathematics.
The earliest mathematicians were from Africa and female?.
The earliest artifact globally, which demonstrated counting was a fibula of a baboon, dated 35 000 BC, which had 29 notches carved into it. It was found in the Lembombo mountains between South Africa and Swaziland. [1]
Other early artifacts had markings of 28, which has been speculated to be an early count of the menstrual cycle. Were the earliest mathematicians female? The archaeological evidence certainly seems to suggest this.
Tally marks, dated from 20 000 to 8000 BC have been found the in the Democratic Republic of Congo (DRC), which show a knowledge of prime numbers and were already using base-10 counting, which is the basis of much of applied mathematics and physics today.
Many of the traditional games also show a knowledge of probability. [For example Tchadji and Muravarava from Mozambique]
The earliest recorded female mathematician in the world was Hypatia, who was born in Alexandria in Egypt, while it was still under Greek occupation. She was killed in 415 AD by Christian fundamentalists. Much of her work was destroyed by the invading Romans. She was a mathematician, astronomer and philosopher. She gave lessons in conical sections and edited various mathematical texts. She also gave lessons on the construction of the astrolabe, which was used for more than 1000 years to map the stars, surveying and sea navigation at night. Her work helped to lay the foundation for the later work of Descarte and Isaac Newton. [2]
Oral tradition and weaving as a means of preserving sona geometry
While the earliest mathematicians may have been female, the rise of patriarchal society placed mathematical knowledge primarily in the hands of males. There is evidence that at the time of the Roman empire there was artwork based on meander patterns, which is also part of knot theory. [3] At the same time there was evidence of sona patterns and knot theory in South India, Southern Africa and Celtic society. These developments were independent of one another. The sona patterns from Southern Africa demonstrated a geometry arguably far more advanced and abstract mathematics than the Euclidean geometry of the ancient Greeks. Yet, the knowledge of these highly complex patterns predate written history and were preserved through story-telling among male hunters and male initiation ceremonies. There were male experts, the akwa kuta sona, who ensured that oral history preserved the gains of mathematical thought. [4] It could be argued that the free labour of subject women subsidised the preservation of sona mathematics. The Yombe women in the Congo used their knowledge of sona geometry to weave intricate designs in mats. This art form also served as a means of transmitting knowledge from one generation to the next. In ancient Greek and Roman society it was the unpaid slave labour that subsidised their ethnic cultural development, of which the mathematical sciences was part.
As colonial and neo-colonial society developed and disrupted the oral and art traditions, there is a danger that many of the earlier theoretical advances in mathematics may be lost.
What are sona patterns?
‘Although their sona (singular “lusona”) drawings arise in several different forms, one of the more common, and the most mathematical, can be viewed as a grid of dots with a curve passing through the grid, “bouncing” off the boundary and off internal “mirrors,” to create a single continuous curve.’ [5]
They can be in the form of monolinear (one line) or several lines enclosing all designated points without repeating itself.
For example, there are at least 3 ways of enclosing this array of 5 dots with a single line. They are from 3 different families of line spaces.
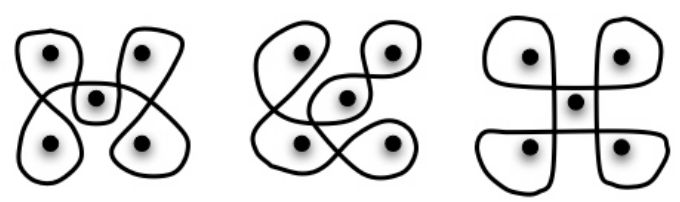(Journal of Mathematics and Art, March 2010) [6]
Some of the uses of sona geometry today
Sona geometry forms part of knot theory which has applications which enable accurate DNA mapping. It also assists in the accurate construction of organic compounds, e.g., in the development of new medicines. For example, the use of the incorrect mirror image of a compound in a medicine can have totally different outcomes, even if the chemical composition is exactly as required. Sona geometry has various applications in nanotechnology and physics.For example, it provides a useful tool in examining patterns in the Sun’s corona. [7]
Sadly, the full scope of sona geometry which has been passed down from generation to generation through oral and art traditions, in regions such as Angola, the DRC, Zambia and Mozambique, has not been fully recorded and catalogued
Introductory exercises:
Consider the dots on the 6 faces of a regular die. Using pen and paper, or a patch of sand and your finger, can you draw a sona pattern, surrounding each dot, using a single line, without lifting your pen (or your finger), without the pattern going over itself more than once? Try the patterns of each of the 6 separately.
Why not experiment with a square array of dots and a rectangular array of dots.
Welcome to the world of sona geometry.
Some more complex patterns
Now that you have tried some of your own patterns, you will appreciate the sona patterns done by our expert akwa kuta sona. Here are some samples drawn mainly from Pinterest and other references below:
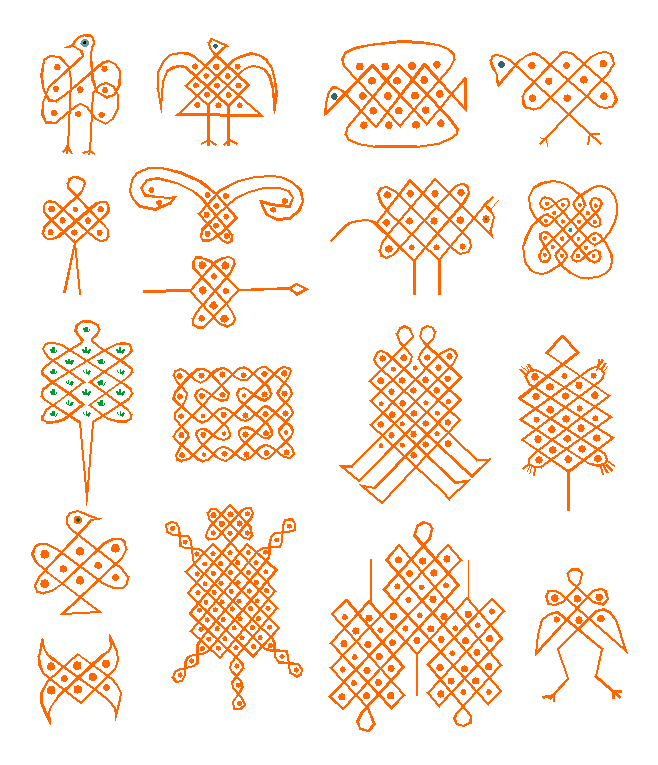Pinterest, (sd) [8]
Pinterest (sd) [9]
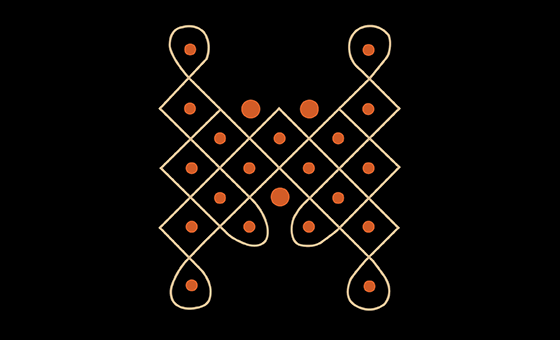(Kleber Kithian, sd) [10]
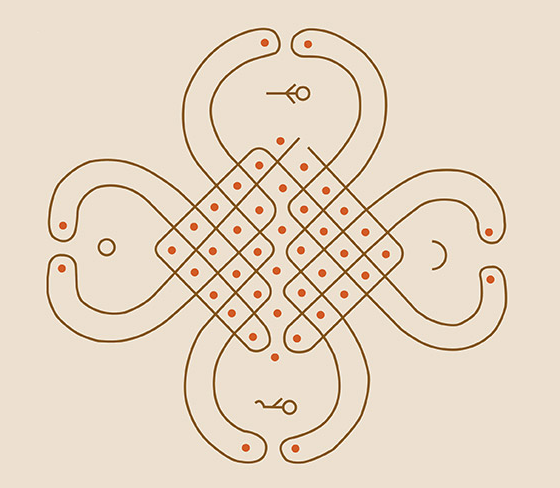(Kleber Kithian, sd) [11]
Future challenges
Mathematics should not be limited or regarded as the domain of males. Everyone can do mathematics. Basket weaving involving sona patterns could be seen as a resistance by females against male monopoly of mathematical knowledge. This needs to be extended. We need mathematics for the billions, not an elite.
It is our task to integrate sona geometry into our school and university syllabi. After all, this is a branch of modern mathematics and is a living example of the contribution of African mathematics to world culture. Accurate DNA mapping as well as accurate production of new medicines require knowledge and application of sona geometry. [12]It is a step towards not only the decolonisation of mathematics but acceptance that African mathematics contributes in a real way to and is integral to modern Mathematics and Science. [13]
Further, the development of mathematics and science is an international task. It is incumbent on us to launch a project to systematically record all the remaining sona patterns which are currently in the hands of the last remaining akwa kuta sona and the female weaver-artists. Who knows, perhaps several mathematical proofs of current challenges may already exist?
Endnotes
[1] Paulus Gerdes, On Mathematics in the History of Sub-Saharan Africa. (Historia Mathematica 21, 1994). pp 345- 376. ↵
[2] Ginny Aldair, Biography of Women Mathematicians: Hypatia. (Agnes Scott College, 1995) https://www.agnesscott.edu/lriddle/women/hypatia.htm acessed 28th August 2018. ↵
[3] Liu, Yang, and Godfried Toussaint. "Unravelling Roman Mosaic Meander Patterns: A Simple Algorithm For Their Generation". Journal Of Mathematics And The Arts 4 (1): (2010) 1-11. doi:10.1080/17513470903311644. https://www.researchgate.net/publication/228562827 accessed 24 June 2018 ↵
[4] Paulus Gerdes, Ethnomathematics and Education in Africa. Second edition: (ISTEG Belo Horizonte Boane Mozambique.2014). http://www.lulu.com/spotlight/pgerdes accessed 26 June 2018 ↵
[5] Darrah Chavey, Mathematical Experiments with African Sona Designs. (sine datum)
https://www.beloit.edu/computerscience/faculty/chavey/sonaExperiments/ accessed 25 June 2018. ↵
[6] Liu Yang, 2010 ↵
[7] Dorothy and Erica Flapan, (Eds) Proceedings of Symposia in Applied Mathematics, Vol 66 Jan 2-4, Applications of Knot Theory. American Mathematical Society, San Diego, California (2008). ↵
[8] Pinterest (sd) https://za.pinterest.com/pin/564920346978414053/ accessed 30 June 2018 ↵
[9] Pinterest (sd) https://za.pinterest.com/pin/183521753540006561/ accessed 30 June 2018 ↵
[10] Kleber Kithian, The art of storytelling in Drawings and the Theorem of Pythagoras, (O Baricentro da Mente, sd) https://www.obaricentrodamente.com/2015/11/a-arte-de-contar-historias-em-desenhos.html accessed 30 June 2018. ↵
[11] “Ibid” ↵
[12] Kunio Murasugi, Translated by Bohdan Kurpita, Knot theory and its application. Publisher: Birkhauser (Boston, Basel, Berlin, 1996) ↵
[13] Darrah Chavey, Wallpaper designs of Mirror Curves inspired by African Sona, (Beloit College, sd) https://www.beloit.edu/computerscience/assets/Wallpaper_Sona.pdf , accessed 10 July 2018. ↵